#математика
Математика в ML: объясняю на пиве
Итак, ваш друг спросил вас: «Какую математику нужно знать, чтобы заниматься машинным обучением?». Можно сколько угодно раз отвечать на этот вопрос, а вопрос все равно останется, и будет задаваться снова и снова. Так давайте научимся на этот вопрос отвечать.
Часть 1. Математический анализ и линейная алгебра
🍺 Что делает машинное обучение? На основе известных примеров учится прогнозировать правильные ответы на новых примерах. Ну например, вы знаете население в окрестности 500 метров каждого магазина большой ритейловой сети (обозначим x1 для первого магазина, x2 для второго и так далее) и знаете сколько пива (естественно, безалкогольного) продают в каждом магазине за год (обозначим y1, y2 и так далее для всех магазинов). И вот вы хотите открыть новый магазин, рядом с которым будет жить х человек. Вы резонно предполагаете, что если х = 0, наверно и продажи будут примерно нулевые (конечно не факт, но примем для простоты) и решаете, что будете пересчитывать людей в пиво по формуле f(x) = a * x. Остается найти коэффициент а.
📉Ну что ж, мы хотим, чтобы ошибка прогноза хотя бы на известных нам примерах была как можно меньше. Т.е. например для первого магазина (y1 - f(x1)) было как можно меньше. Но, строго говоря, «как можно меньше» это немного кривая формулировка, если (y1 - f(x1)) будет большим по модулю но отрицательным числом - это нам не подойдет, значит мы сильно промахиваемся. Поэтому давайте смотреть на квадрат этого выражения: (y1 - f(x1))^2. Квадрат уж если будет маленьким, то тогда (y1 - f(x1)) будет близким к нулю, а значит мы будем мало ошибаться.
🌡️ Остается последний вопрос: что нам важнее - минимизировать ошибку прогноза на первом магазине (y1 - f(x1))^2, на втором (y2 - f(x2))^2, на третьем или еще на каком-то? Конечно же, мы хотим мало ошибаться в среднем. Отсюда легко придумать, каким надо подбирать наш коэффициент перевода людей в пиво a - таким, чтобысредняя температура по больнице средняя ошибка на обучающей выборке была как можно меньше:
((y1 - f(x1))^2 + (y2 - f(x2))^2 + ... + (yN - f(xN))^2) / N -> min
Ну что же, выражение выше, когда все x и y известны, можно рассмотреть как выражение, зависящее от а, т.е. мы имеем задачу вида L(a) -> min. Значит самое главное, что нам нужно из математики - уметь решать такие задачи.
👦 В нашем примере даже старательный десятиклассник (а иногда и девятиклассник) без проблем скажет: надо посчитать производную L(a), приравнять ее к нулю и получить готовую формулу для a. И это правда решит нашу проблему. Чуточку хуже будет, если мы прогнозируем потребление народом пива (безалкогольного!) не только по населению в окрестности магазина, но и по другим важным факторам (насколько в этом году будет теплое лето, какой средний доход у населения вокруг магазина, а есть ли рядом оживленные дороги и какой через них проезжает поток людей, есть ли рядом другие магазины и так далее).
👨🏫 В этом случае мы можем захотеть строить прогнозы вида f(x[1], x[2], ..., x[d]) = a1 * x[1] + a2 * x[2] + ... + ad * x[d], где d - количество признаков, используемых в прогнозе. Тогда наша задача принимает вид L(a1, a2, ..., ad) -> min, а это уже поиск экстремума функции от d переменных. Оказывается, на первом курсе матанализа студентам рассказывают, что тут можно действовать почти также, как в школе: только производную теперь нужно считать и приравнивать к нулю по каждой переменной. Например, всем известная готовая формула весов в линейной регрессии и получается таким образом. Более того, человек, окультуренный линейной алгеброй, а точнее знающий, что такое матрицы и как их перемножать, сможет получить эту формулу буквально в несколько строчек (см. рис.). Вот и матрицы пригодились.
Но это если наша функция L(a1, a2, ..., ad) красивая и простая. А если наша функция - какая-то страхолюдина (а в ML столько всего напридумывали), то выписать готовую формулу для коэффициентов уже сложно. И тут на помощь приходят численные методы оптимизации. В начале погружения в ML знать какие-то особые методы не обязательно, достаточно градиентного спуска.
Математика в ML: объясняю на пиве
Итак, ваш друг спросил вас: «Какую математику нужно знать, чтобы заниматься машинным обучением?». Можно сколько угодно раз отвечать на этот вопрос, а вопрос все равно останется, и будет задаваться снова и снова. Так давайте научимся на этот вопрос отвечать.
Часть 1. Математический анализ и линейная алгебра
🍺 Что делает машинное обучение? На основе известных примеров учится прогнозировать правильные ответы на новых примерах. Ну например, вы знаете население в окрестности 500 метров каждого магазина большой ритейловой сети (обозначим x1 для первого магазина, x2 для второго и так далее) и знаете сколько пива (естественно, безалкогольного) продают в каждом магазине за год (обозначим y1, y2 и так далее для всех магазинов). И вот вы хотите открыть новый магазин, рядом с которым будет жить х человек. Вы резонно предполагаете, что если х = 0, наверно и продажи будут примерно нулевые (конечно не факт, но примем для простоты) и решаете, что будете пересчитывать людей в пиво по формуле f(x) = a * x. Остается найти коэффициент а.
📉Ну что ж, мы хотим, чтобы ошибка прогноза хотя бы на известных нам примерах была как можно меньше. Т.е. например для первого магазина (y1 - f(x1)) было как можно меньше. Но, строго говоря, «как можно меньше» это немного кривая формулировка, если (y1 - f(x1)) будет большим по модулю но отрицательным числом - это нам не подойдет, значит мы сильно промахиваемся. Поэтому давайте смотреть на квадрат этого выражения: (y1 - f(x1))^2. Квадрат уж если будет маленьким, то тогда (y1 - f(x1)) будет близким к нулю, а значит мы будем мало ошибаться.
🌡️ Остается последний вопрос: что нам важнее - минимизировать ошибку прогноза на первом магазине (y1 - f(x1))^2, на втором (y2 - f(x2))^2, на третьем или еще на каком-то? Конечно же, мы хотим мало ошибаться в среднем. Отсюда легко придумать, каким надо подбирать наш коэффициент перевода людей в пиво a - таким, чтобы
((y1 - f(x1))^2 + (y2 - f(x2))^2 + ... + (yN - f(xN))^2) / N -> min
Ну что же, выражение выше, когда все x и y известны, можно рассмотреть как выражение, зависящее от а, т.е. мы имеем задачу вида L(a) -> min. Значит самое главное, что нам нужно из математики - уметь решать такие задачи.
👦 В нашем примере даже старательный десятиклассник (а иногда и девятиклассник) без проблем скажет: надо посчитать производную L(a), приравнять ее к нулю и получить готовую формулу для a. И это правда решит нашу проблему. Чуточку хуже будет, если мы прогнозируем потребление народом пива (безалкогольного!) не только по населению в окрестности магазина, но и по другим важным факторам (насколько в этом году будет теплое лето, какой средний доход у населения вокруг магазина, а есть ли рядом оживленные дороги и какой через них проезжает поток людей, есть ли рядом другие магазины и так далее).
👨🏫 В этом случае мы можем захотеть строить прогнозы вида f(x[1], x[2], ..., x[d]) = a1 * x[1] + a2 * x[2] + ... + ad * x[d], где d - количество признаков, используемых в прогнозе. Тогда наша задача принимает вид L(a1, a2, ..., ad) -> min, а это уже поиск экстремума функции от d переменных. Оказывается, на первом курсе матанализа студентам рассказывают, что тут можно действовать почти также, как в школе: только производную теперь нужно считать и приравнивать к нулю по каждой переменной. Например, всем известная готовая формула весов в линейной регрессии и получается таким образом. Более того, человек, окультуренный линейной алгеброй, а точнее знающий, что такое матрицы и как их перемножать, сможет получить эту формулу буквально в несколько строчек (см. рис.). Вот и матрицы пригодились.
Но это если наша функция L(a1, a2, ..., ad) красивая и простая. А если наша функция - какая-то страхолюдина (а в ML столько всего напридумывали), то выписать готовую формулу для коэффициентов уже сложно. И тут на помощь приходят численные методы оптимизации. В начале погружения в ML знать какие-то особые методы не обязательно, достаточно градиентного спуска.
🔥49👍19❤15👏3🤯1
tg-me.com/kantor_ai/252
Create:
Last Update:
Last Update:
#математика
Математика в ML: объясняю на пиве
Итак, ваш друг спросил вас: «Какую математику нужно знать, чтобы заниматься машинным обучением?». Можно сколько угодно раз отвечать на этот вопрос, а вопрос все равно останется, и будет задаваться снова и снова. Так давайте научимся на этот вопрос отвечать.
Часть 1. Математический анализ и линейная алгебра
🍺 Что делает машинное обучение? На основе известных примеров учится прогнозировать правильные ответы на новых примерах. Ну например, вы знаете население в окрестности 500 метров каждого магазина большой ритейловой сети (обозначим x1 для первого магазина, x2 для второго и так далее) и знаете сколько пива (естественно, безалкогольного) продают в каждом магазине за год (обозначим y1, y2 и так далее для всех магазинов). И вот вы хотите открыть новый магазин, рядом с которым будет жить х человек. Вы резонно предполагаете, что если х = 0, наверно и продажи будут примерно нулевые (конечно не факт, но примем для простоты) и решаете, что будете пересчитывать людей в пиво по формуле f(x) = a * x. Остается найти коэффициент а.
📉Ну что ж, мы хотим, чтобы ошибка прогноза хотя бы на известных нам примерах была как можно меньше. Т.е. например для первого магазина (y1 - f(x1)) было как можно меньше. Но, строго говоря, «как можно меньше» это немного кривая формулировка, если (y1 - f(x1)) будет большим по модулю но отрицательным числом - это нам не подойдет, значит мы сильно промахиваемся. Поэтому давайте смотреть на квадрат этого выражения: (y1 - f(x1))^2. Квадрат уж если будет маленьким, то тогда (y1 - f(x1)) будет близким к нулю, а значит мы будем мало ошибаться.
🌡️ Остается последний вопрос: что нам важнее - минимизировать ошибку прогноза на первом магазине (y1 - f(x1))^2, на втором (y2 - f(x2))^2, на третьем или еще на каком-то? Конечно же, мы хотим мало ошибаться в среднем. Отсюда легко придумать, каким надо подбирать наш коэффициент перевода людей в пиво a - таким, чтобысредняя температура по больнице средняя ошибка на обучающей выборке была как можно меньше:
((y1 - f(x1))^2 + (y2 - f(x2))^2 + ... + (yN - f(xN))^2) / N -> min
Ну что же, выражение выше, когда все x и y известны, можно рассмотреть как выражение, зависящее от а, т.е. мы имеем задачу вида L(a) -> min. Значит самое главное, что нам нужно из математики - уметь решать такие задачи.
👦 В нашем примере даже старательный десятиклассник (а иногда и девятиклассник) без проблем скажет: надо посчитать производную L(a), приравнять ее к нулю и получить готовую формулу для a. И это правда решит нашу проблему. Чуточку хуже будет, если мы прогнозируем потребление народом пива (безалкогольного!) не только по населению в окрестности магазина, но и по другим важным факторам (насколько в этом году будет теплое лето, какой средний доход у населения вокруг магазина, а есть ли рядом оживленные дороги и какой через них проезжает поток людей, есть ли рядом другие магазины и так далее).
👨🏫 В этом случае мы можем захотеть строить прогнозы вида f(x[1], x[2], ..., x[d]) = a1 * x[1] + a2 * x[2] + ... + ad * x[d], где d - количество признаков, используемых в прогнозе. Тогда наша задача принимает вид L(a1, a2, ..., ad) -> min, а это уже поиск экстремума функции от d переменных. Оказывается, на первом курсе матанализа студентам рассказывают, что тут можно действовать почти также, как в школе: только производную теперь нужно считать и приравнивать к нулю по каждой переменной. Например, всем известная готовая формула весов в линейной регрессии и получается таким образом. Более того, человек, окультуренный линейной алгеброй, а точнее знающий, что такое матрицы и как их перемножать, сможет получить эту формулу буквально в несколько строчек (см. рис.). Вот и матрицы пригодились.
Но это если наша функция L(a1, a2, ..., ad) красивая и простая. А если наша функция - какая-то страхолюдина (а в ML столько всего напридумывали), то выписать готовую формулу для коэффициентов уже сложно. И тут на помощь приходят численные методы оптимизации. В начале погружения в ML знать какие-то особые методы не обязательно, достаточно градиентного спуска.
Математика в ML: объясняю на пиве
Итак, ваш друг спросил вас: «Какую математику нужно знать, чтобы заниматься машинным обучением?». Можно сколько угодно раз отвечать на этот вопрос, а вопрос все равно останется, и будет задаваться снова и снова. Так давайте научимся на этот вопрос отвечать.
Часть 1. Математический анализ и линейная алгебра
🍺 Что делает машинное обучение? На основе известных примеров учится прогнозировать правильные ответы на новых примерах. Ну например, вы знаете население в окрестности 500 метров каждого магазина большой ритейловой сети (обозначим x1 для первого магазина, x2 для второго и так далее) и знаете сколько пива (естественно, безалкогольного) продают в каждом магазине за год (обозначим y1, y2 и так далее для всех магазинов). И вот вы хотите открыть новый магазин, рядом с которым будет жить х человек. Вы резонно предполагаете, что если х = 0, наверно и продажи будут примерно нулевые (конечно не факт, но примем для простоты) и решаете, что будете пересчитывать людей в пиво по формуле f(x) = a * x. Остается найти коэффициент а.
📉Ну что ж, мы хотим, чтобы ошибка прогноза хотя бы на известных нам примерах была как можно меньше. Т.е. например для первого магазина (y1 - f(x1)) было как можно меньше. Но, строго говоря, «как можно меньше» это немного кривая формулировка, если (y1 - f(x1)) будет большим по модулю но отрицательным числом - это нам не подойдет, значит мы сильно промахиваемся. Поэтому давайте смотреть на квадрат этого выражения: (y1 - f(x1))^2. Квадрат уж если будет маленьким, то тогда (y1 - f(x1)) будет близким к нулю, а значит мы будем мало ошибаться.
🌡️ Остается последний вопрос: что нам важнее - минимизировать ошибку прогноза на первом магазине (y1 - f(x1))^2, на втором (y2 - f(x2))^2, на третьем или еще на каком-то? Конечно же, мы хотим мало ошибаться в среднем. Отсюда легко придумать, каким надо подбирать наш коэффициент перевода людей в пиво a - таким, чтобы
((y1 - f(x1))^2 + (y2 - f(x2))^2 + ... + (yN - f(xN))^2) / N -> min
Ну что же, выражение выше, когда все x и y известны, можно рассмотреть как выражение, зависящее от а, т.е. мы имеем задачу вида L(a) -> min. Значит самое главное, что нам нужно из математики - уметь решать такие задачи.
👦 В нашем примере даже старательный десятиклассник (а иногда и девятиклассник) без проблем скажет: надо посчитать производную L(a), приравнять ее к нулю и получить готовую формулу для a. И это правда решит нашу проблему. Чуточку хуже будет, если мы прогнозируем потребление народом пива (безалкогольного!) не только по населению в окрестности магазина, но и по другим важным факторам (насколько в этом году будет теплое лето, какой средний доход у населения вокруг магазина, а есть ли рядом оживленные дороги и какой через них проезжает поток людей, есть ли рядом другие магазины и так далее).
👨🏫 В этом случае мы можем захотеть строить прогнозы вида f(x[1], x[2], ..., x[d]) = a1 * x[1] + a2 * x[2] + ... + ad * x[d], где d - количество признаков, используемых в прогнозе. Тогда наша задача принимает вид L(a1, a2, ..., ad) -> min, а это уже поиск экстремума функции от d переменных. Оказывается, на первом курсе матанализа студентам рассказывают, что тут можно действовать почти также, как в школе: только производную теперь нужно считать и приравнивать к нулю по каждой переменной. Например, всем известная готовая формула весов в линейной регрессии и получается таким образом. Более того, человек, окультуренный линейной алгеброй, а точнее знающий, что такое матрицы и как их перемножать, сможет получить эту формулу буквально в несколько строчек (см. рис.). Вот и матрицы пригодились.
Но это если наша функция L(a1, a2, ..., ad) красивая и простая. А если наша функция - какая-то страхолюдина (а в ML столько всего напридумывали), то выписать готовую формулу для коэффициентов уже сложно. И тут на помощь приходят численные методы оптимизации. В начале погружения в ML знать какие-то особые методы не обязательно, достаточно градиентного спуска.
BY Kantor.AI
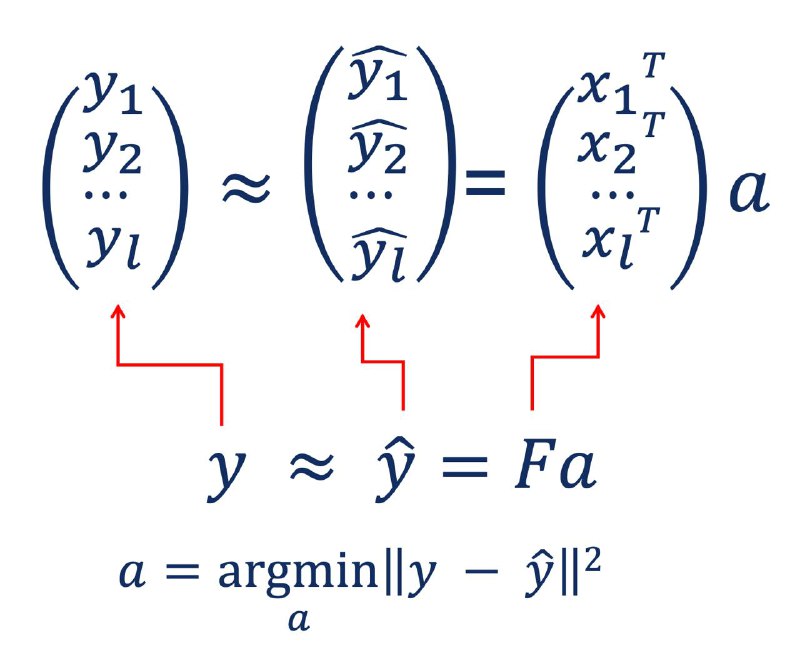
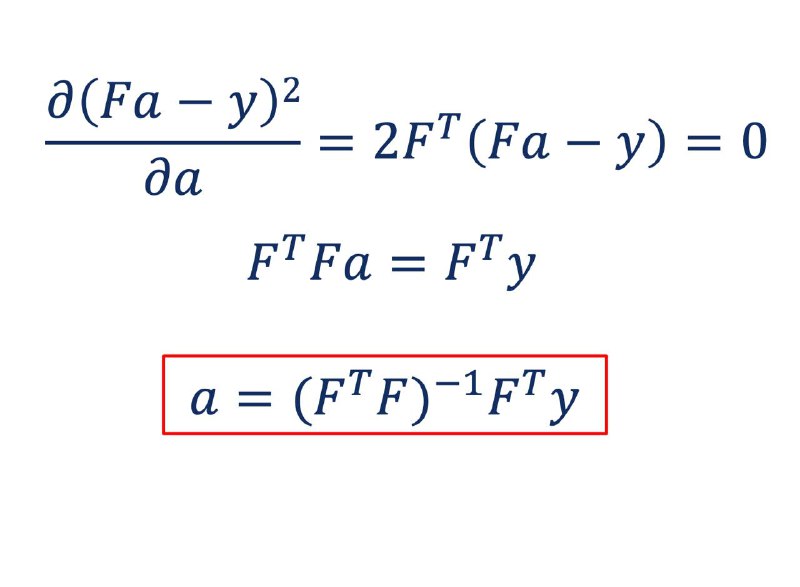
Share with your friend now:
tg-me.com/kantor_ai/252
